Функция с дробным показателем. Степенная функция и ее свойства

Степенной называется функция вида y=x n (читается как y равно х в степени n), где n – некоторое заданное число. Частными случаями степенных функций является функции вида y=x, y=x 2 , y=x 3 , y=1/x и многие другие. Расскажем подробнее о каждой из них.

Линейная функция y=x 1 (y=x)

График прямая линия, проходящая через точку (0;0) под углом 45 градусов к положительному направлению оси Ох.

График представлен ниже.

Основные свойства линейной функции:

Функция возрастающая и определена на всей числовой оси.
Не имеет максимального и минимального значений.

Квадратичная функция y=x 2

Графиком квадратичной функции является парабола.

Основные свойства квадратичной функции:

1. При х =0, у=0, и у>0 при х0
2. Минимальное значение квадратичная функция достигает в своей вершине. Ymin при x=0; Следует также заметить, что максимального значения у функции не существует.

3. Функция убывает на промежутке (-∞;0] и возрастает на промежутке \[{\mathop{lim}_{x\to +\infty } x^{2n}\ }=+\infty \]

График (рис. 2).

Рисунок 2. График функции $f\left(x\right)=x^{2n}$

Свойства степенной функции с натуральным нечетным показателем

Область определения -- все действительные числа.

$f\left(-x\right)={(-x)}^{2n-1}={-x}^{2n}=-f(x)$ -- функция нечетна.

$f(x)$ - непрерывна на всей области определения.

Область значения -- все действительные числа.

$f"\left(x\right)=\left(x^{2n-1}\right)"=(2n-1)\cdot x^{2(n-1)}\ge 0$

Функция возрастает на всей области определения.

$f\left(x\right)0$, при $x\in (0,+\infty)$.

$f{""\left(x\right)}={\left(\left(2n-1\right)\cdot x^{2\left(n-1\right)}\right)}"=2\left(2n-1\right)(n-1)\cdot x^{2n-3}$

\ \

Функция вогнута, при $x\in (-\infty ,0)$ и выпукла, при $x\in (0,+\infty)$.

График (рис. 3).

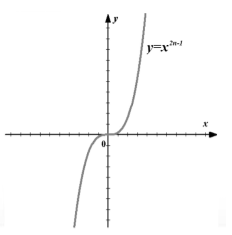
Рисунок 3. График функции $f\left(x\right)=x^{2n-1}$

Степенная функция с целым показателем

Для начала введем понятие степени с целым показателем.

Определение 3

Степень действительного числа $a$ c целым показателем $n$ определяется формулой:

Рисунок 4.

Рассмотрим теперь степенную функцию с целым показателем, её свойства и график.

Определение 4

$f\left(x\right)=x^n$ ($n\in Z)$ называется степенной функцией с целым показателем.

Если степень больше нуля, то мы приходим к случаю степенной функции с натуральным показателем. Его мы уже рассмотрели выше. При $n=0$ мы получим линейную функцию $y=1$. Её рассмотрение оставим читателю. Осталось рассмотреть свойства степенной функции с отрицательным целым показателем

Свойства степенной функции с отрицательным целым показателем

Область определения -- $\left(-\infty ,0\right)(0,+\infty)$.

Если показатель четный, то функция четна, если нечетный, то функция нечетна.

$f(x)$ - непрерывна на всей области определения.

Область значения:

Если показатель четный, то $(0,+\infty)$, если нечетный, то $\left(-\infty ,0\right)(0,+\infty)$.

При нечетном показателе функция убывает, при $x\in \left(-\infty ,0\right)(0,+\infty)$. При четном показателе функция убывает при $x\in (0,+\infty)$. и возрастает, при $x\in \left(-\infty ,0\right)$.

$f(x)\ge 0$ на всей области определения

Приведены справочные данные по показательной функции - основные свойства, графики и формулы. Рассмотрены следующие вопросы: область определения, множество значений, монотонность, обратная функция, производная, интеграл, разложение в степенной ряд и представление посредством комплексных чисел.

Определение

Показательная функция - это обобщение произведения n чисел, равных a :
y(n) = a n = a·a·a···a ,
на множество действительных чисел x :
y(x) = a x .
Здесь a - фиксированное действительное число, которое называют основанием показательной функции .
Показательную функцию с основанием a также называют экспонентой по основанию a .

Обобщение выполняется следующим образом.
При натуральном x = 1, 2, 3,... , показательная функция является произведением x множителей:
.
При этом она обладает свойствами (1.5-8) (), которые следуют из правил умножения чисел. При нулевом и отрицательных значениях целых чисел , показательную функцию определяют по формулам (1.9-10). При дробных значениях x = m/n рациональных чисел, , ее определяют по формуле(1.11). Для действительных , показательную функцию определяют как предел последовательности:
,
где - произвольная последовательность рациональных чисел, сходящаяся к x : .
При таком определении, показательная функция определена для всех , и удовлетворяет свойствам (1.5-8), как и для натуральных x .

Строгая математическая формулировка определения показательной функции и доказательство ее свойств приводится на странице «Определение и доказательство свойств показательной функции ».

Свойства показательной функции

Показательная функция y = a x , имеет следующие свойства на множестве действительных чисел () :
(1.1) определена и непрерывна, при , для всех ;
(1.2) при a ≠ 1 имеет множество значений ;
(1.3) строго возрастает при , строго убывает при ,
является постоянной при ;
(1.4) при ;
при ;
(1.5) ;
(1.6) ;
(1.7) ;
(1.8) ;
(1.9) ;
(1.10) ;
(1.11) , .

Другие полезные формулы.
.
Формула преобразования к показательной функции с другим основанием степени:

При b = e , получаем выражение показательной функции через экспоненту:

Частные значения

, , , , .

На рисунке представлены графики показательной функции
y(x) = a x
для четырех значений основания степени : a = 2 , a = 8 , a = 1/2 и a = 1/8 . Видно, что при a > 1 показательная функция монотонно возрастает. Чем больше основание степени a , тем более сильный рост. При 0 < a < 1 показательная функция монотонно убывает. Чем меньше показатель степени a , тем более сильное убывание.

Возрастание, убывание

Показательная функция, при является строго монотонной, поэтому экстремумов не имеет. Основные ее свойства представлены в таблице.

	y = a x , a > 1	y = a x , 0 < a < 1
Область определения	- ∞ < x < + ∞	- ∞ < x < + ∞
Область значений	0 < y < + ∞	0 < y < + ∞
Монотонность	монотонно возрастает	монотонно убывает
Нули, y = 0	нет	нет
Точки пересечения с осью ординат, x = 0	y = 1	y = 1
	+ ∞	0
	0	+ ∞

Обратная функция

Обратной для показательной функции с основанием степени a является логарифм по основанию a .

Если , то
.
Если , то
.

Дифференцирование показательной функции

Для дифференцирования показательной функции, ее основание нужно привести к числу e , применить таблицу производных и правило дифференцирования сложной функции.

Для этого нужно использовать свойство логарифмов
и формулу из таблицы производных :
.

Пусть задана показательная функция:
.
Приводим ее к основанию e :

Применим правило дифференцирования сложной функции . Для этого вводим переменную

Тогда

Из таблице производных имеем (заменим переменную x на z ):
.
Поскольку - это постоянная, то производная z по x равна
.
По правилу дифференцирования сложной функции:
.

Производная показательной функции

.
Производная n-го порядка:
.
Вывод формул > > >

Пример дифференцирования показательной функции

Найти производную функции
y = 3 5 x

Решение

Выразим основание показательной функции через число e .
3 = e ln 3
Тогда
.
Вводим переменную
.
Тогда

Из таблицы производных находим:
.
Поскольку 5ln 3 - это постоянная, то производная z по x равна:
.
По правилу дифференцирования сложной функции имеем:
.

Ответ

Интеграл

Выражения через комплексные числа

Рассмотрим функцию комплексного числа z :
f(z) = a z
где z = x + iy ; i 2 = - 1 .
Выразим комплексную постоянную a через модуль r и аргумент φ :
a = r e i φ
Тогда

.
Аргумент φ определен не однозначно. В общем виде
φ = φ 0 + 2 πn ,
где n - целое. Поэтому функция f(z) также не однозначна. Часто рассматривают ее главное значение
.

Разложение в ряд

Использованная литература:
И.Н. Бронштейн, К.А. Семендяев, Справочник по математике для инженеров и учащихся втузов, «Лань», 2009.

1. Степенная функция, ее свойства и график;

2. Преобразования:

Параллельный перенос;

Симметрия относительно осей координат;

Симметрия относительно начала координат;

Симметрия относительно прямой y = x;

Растяжение и сжатие вдоль осей координат.

3. Показательная функция, ее свойства и график, аналогичные преобразования;

4. Логарифмическая функция , ее свойства и график;

5. Тригонометрическая функция, ее свойства и график, аналогичные преобразования (y = sin x; y = cos x; y = tg x);

Функция: y = x\n - ее свойства и график.

Степенная функция, ее свойства и график

y = x, y = x 2 , y = x 3 , y = 1/x и т. д. Все эти функции являются частными случаями степенной функции, т. е. функции y = x p , где p - заданное действительное число.
Свойства и график степенной функции существенно зависит от свойств степени с действительным показателем, и в частности от того, при каких значениях x и p имеет смысл степень x p . Перейдем к подобному рассмотрению различных случаев в зависимости от
показателя степени p.

Показатель p = 2n - четное натуральное число.

y = x 2n , где n - натуральное число, обладает следующими свойствами:

область определения - все действительные числа, т. е. множество R;
множество значений - неотрицательные числа, т. е. y больше или равно 0;
функция y = x 2n четная, так как x 2n = (-x) 2n
функция является убывающей на промежутке x < 0 и возрастающей на промежутке x > 0.

График функции y = x 2n имеет такой же вид, как например график функции y = x 4 .

2. Показатель p = 2n - 1 - нечетное натуральное число

В этом случае степенная функция y = x 2n-1 , где натуральное число, обладает следующими свойствами:

область определения - множество R;
множество значений - множество R;
функция y = x 2n-1 нечетная, так как (-x) 2n-1 = x 2n-1 ;
функция является возрастающей на всей действительной оси.

График функции y = x 2n-1 y = x 3 .

3. Показатель p = -2n , где n - натуральное число.

В этом случае степенная функция y = x -2n = 1/x 2n обладает следующими свойствами:

множество значений - положительные числа y>0;
функция y = 1/x 2n четная, так как 1/(-x) 2n = 1/x 2n ;
функция является возрастающей на промежутке x0.

График функции y = 1/x 2n имеет такой же вид, как, например, график функции y = 1/x 2 .

4. Показатель p = -(2n-1) , где n - натуральное число.
В этом случае степенная функция y = x -(2n-1) обладает следующими свойствами:

область определения - множество R, кроме x = 0;
множество значений - множество R, кроме y = 0;
функция y = x -(2n-1) нечетная, так как (-x) -(2n-1) = -x -(2n-1) ;
функция является убывающей на промежутках x < 0 и x > 0 .

График функции y = x -(2n-1) имеет такой же вид, как, например, график функции y = 1/x 3 .

Категории

Популярное